|
|
泻药。实验室最近人人都在做扩散,从连续到离散,从CV到NLP,基本上都被diffusion洗了一遍。但是观察发现,里面的数学基础并不是模型应用的必须。其实大部分的研究者都不需要理解扩散模型的数学本质,更需要的是对扩散模型的原理的经验化理解,从而应用到research里面去。笔者做VAE和diffussion也有一段时间了,就在这里通俗地解释一下diffusion的来龙去脉。
<hr/>Variational AutoEncoder (VAE)
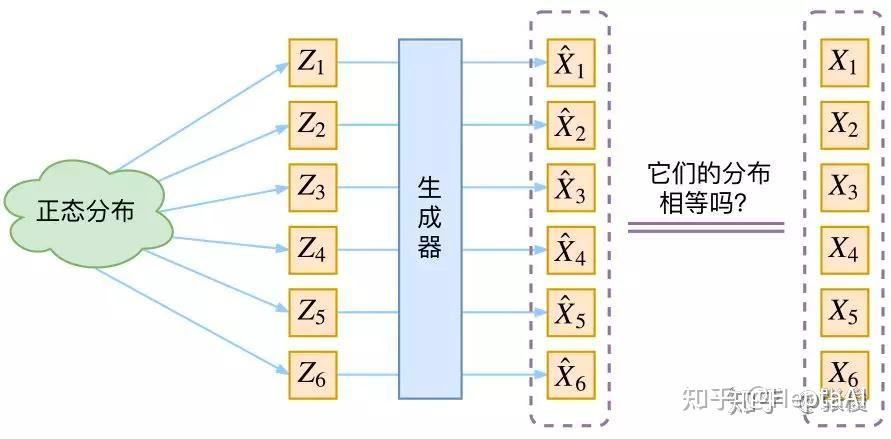
要讲扩散模型,不得不提VAE。VAE和GAN一样,都是从隐变量 Z 生成目标数据 X 。它们假设隐变量服从某种常见的概率分布(比如正态分布),然后希望训练一个模型 X=g(Z) ,这个模型将原来的概率分布映射到训练集的概率分布,也就是分布的变换。注意,VAE和GAN的本质都是概率分布的映射。大致思路如下图所示:
图片来源:https://zhuanlan.zhihu.com/p/34998569
换句话说,大致意思就是先用某种分布随机生成一组隐变量,然后这个隐变量会经过一个生成器生成一组目标数据。VAE和GAN都希望这组数据的分布 \hat{X} 和目标分布 X 尽量接近。
是不是听上去很work?但是这种方法本质上是难以work的,因为“尽量接近”并没有一个确定的关于 X 和 \hat{X} 的相似度的评判标准。换句话说,这种方法的难度就在于,必须去猜测“它们的分布相等吗”这个问题,而缺少真正interpretable的价值判断。有聪明的同学会问,KL散度不就够了吗?不行,因为KL散度是针对两个已知的概率分布求相似度的,而 \hat{X} 和 X 的概率分布目前都是未知。
GAN的做法就是直接把这个度量标准也学过来就行,相当生猛。但是这样做的问题在于依然不interpretable,非常不优雅。VAE的做法就优雅很多了,我们先来看VAE是怎么做的,理解了VAE以后再去理解Diffussion就很自然了。
到底什么是生成模型?
我们看回生成模型到底是个啥。我们拿到一批sample(称为 X ),想要用 X 学到它的分布 p(X) ,这样就能同时学到没被sample到的数据了,用这个分布 p(X) 就能随意采样,然后获得生成结果。但是这个分布九曲回肠,根本不可能直接获得。所以绕个弯,整一个隐变量 Z ,这东西可以生成 X 。不妨假设 Z 满足正态分布,那就可以先从正态分布里面随便取一个 Z ,然后用 Z 和 X 的关系算出 p(X) 。这里不得不用一下数学公式,因为后面一直要用到(其实也很简单,学过概率学基础一下就看得懂):
p(X)=\sum_Z{p(X|Z)p(Z)}
换句话说,就是不直接求 p(X) ,而是造一个别的变量(好听的名字叫“隐变量”),获得这个隐变量和我要搞的 X 的关系,也能搞到 p(X) 。注意,上式中,p(X|Z) 称为后验分布, p(Z) 称为先验分布。
VAE的核心
VAE的核心就是,我们不仅假设 p(Z) 是正态分布,而且假设每个 p(X_k|Z) 也是正态分布。什么意思呢?因为 X 是一组采样,其实可以表示成 X=\{X_1,...,X_k\} ,而我们想要针对每个 X_k 获得一个专属于它和 Z 的一个正态分布。换句话说,有 k 个 X sample,就有 k 个正态分布 p(X_k|Z) 。其实也很好理解,每一个采样点当然都需要一个相对 Z 的分布,因为没有任何两个采样点是完全一致的。
那现在就要想方设法获得这 k 个正态分布了。怎么搞?学!拟合!但是要注意,这里的拟合与GAN不同,本质上是在学习 X_k 和 Z 的关系,而非学习比较 X 与 \hat{X} 的标准。
OK,现在问一个小学二年级就知道的问题,已知是正态分布,学什么才能确定这个正态分布?没错,均值和方差。怎么学?有数据啊! Z 不是你自己假设的吗, X_k 是已知的啊,那你就用这俩去学个均值和方差。
好,现在我们已经学到了这 k 个正态分布。那就好说了,直接从 p(Z|X_k) 里面采样一个 Z_k ,学一个generator,就能获得 X_k=g(Z_k) 了。那接下来只需要最小化方差 D^2(\hat{X}_k,X_k) 就行。来看看下面的图,仔细理解一下:
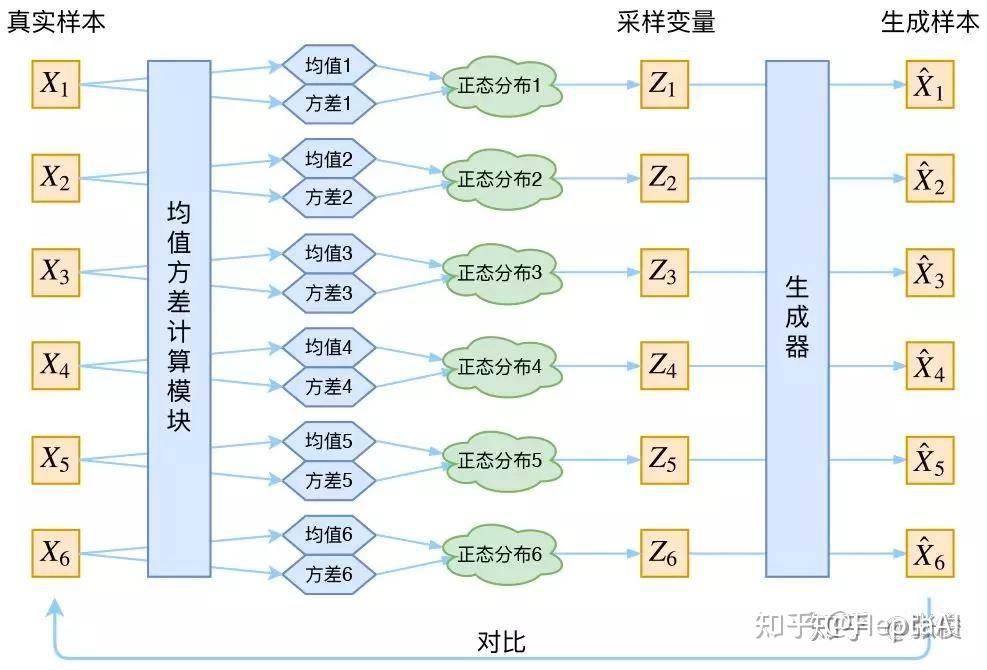
仔细理解的时候有没有发现一个问题?为什么在文章最开头,我们强调了没法直接比较 X 和 \hat{X} 的分布,而在这里,我们认为可以直接比较这俩?注意,这里的 Z_k 是专属于(针对于) X_k 的隐变量,那么和 \hat{X}_k 本身就有对应关系,因此右边的蓝色方框内的“生成器”,是一一对应的生成。
另外,大家可以看到,均值和方差的计算本质上都是encoder。也就是说,VAE其实利用了两个encoder去分别学习均值和方差。
VAE的Variational到底是个啥
这里还有一个非常重要的问题(对于初学者而言可能会比较困难,需要反复思考):由于我们通过最小化 D^2(X_k|\hat{X}_k) 来训练右边的生成器,最终模型会逐渐使得 X_k 和 \hat{X}_k 趋于一致。但是注意,因为 Z_k 是重新随机采样过的,而不是直接通过均值和方差encoder学出来的,这个生成器的输入 Z 是有噪声的。但是仔细思考一下,这个噪声的大小其实就用方差来度量。为了使得分布的学习尽量接近,我们希望噪声越小越好,所以我们会尽量使得方差趋于 0。
但是方差不能为 0,因为我们还想要给模型一些训练难度。如果方差为 0,模型永远只需要学习高斯分布的均值,这样就丢失了随机性,VAE就变成AE了……这就是为什么VAE要在AE前面加一个Variational:我们希望方差能够持续存在,从而带来噪声!那如何解决这个问题呢?其实保证有方差就行,但是VAE给出了一个优雅的答案:不仅需要保证有方差,还要让所有 p(Z|X) 趋于标准正态分布 N(0,I) !为什么要这么做呢?这里又需要一个小小的数学推导:
p(Z)=\sum_X{p(Z|X)p(X)}=N(0,I)p(x)=N(0,I)\sum_Xp(X)=N(0,I)
这条式子大家想必都看得懂,看不懂也没事……关键是结论:如果所有 p(Z|X) 都趋于 N(0,I) ,那么我们可以保证 p(Z) 也趋于 N(0,I) ,从而实现先验的假设,这样就形成了一个闭环!太优雅了!那怎么让所有 p(Z|X) 趋于 N(0,I) 呢?加loss被,具体的loss推导这里就不做深入了,用到了很多数学知识,又要被公式淹没了。到此为止,我们可以把VAE进一步画成:
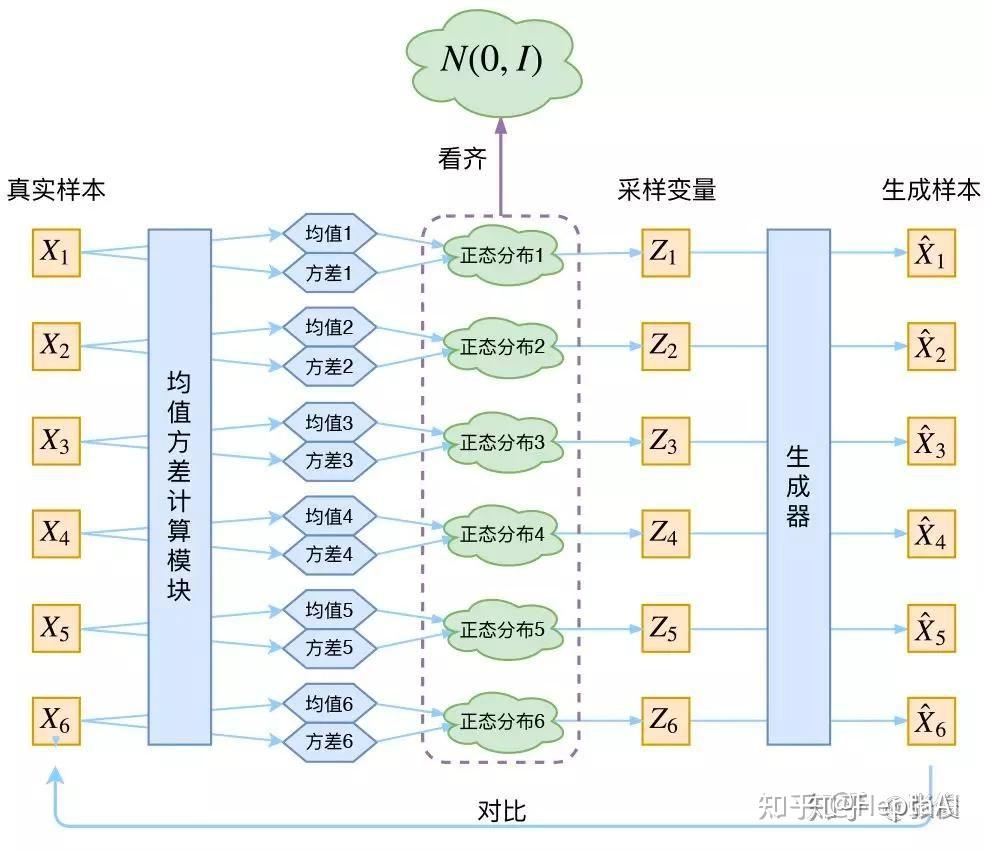
VAE的本质
现在我们来回顾一下VAE到底做了啥。VAE在AE的基础上对均值的encoder添加高斯噪声(正态分布的随机采样),使得decoder(就是右边那个生成器)有噪声鲁棒性;为了防止噪声消失,将所有 p(Z|X) 趋近于标准正态分布,将encoder的均值尽量降为 0,而将方差尽量保持住。这样一来,当decoder训练的不好的时候,整个体系就可以降低噪声;当decoder逐渐拟合的时候,就会增加噪声。
本质上,是不是和GAN很像?!要我命名,我也可以叫VAE是生成对抗encoder(手动滑稽
Diffusion Model(扩散模型,DM)
好了,到此为止,你已经理解了扩散模型的所有基础。现在我们来站在VAE的基础上讲讲扩散模型。目前的教程实在是太数学了,其实可以用更加通俗的语言讲清楚。从本质上说,Diffusion就是VAE的升级版。
VAE有一个做了好几年的核心问题。大家思考一下,上面的VAE中,变分后验 p(X|Z) 是怎么获得的?是学出来的!用 D^2(X_k|\hat{X}_k) 当loss,去学这个 p(X|Z) 。学这个变分后验就有五花八门的方法了,除了上面说的拟合法,还有用纯数学来做的,甚至有用BERT这种PLM来做的。但是无论如何都逃不出这个VAE的框架:必须想办法设计一个生成器 g(Z)=X ,使得变分后验分布 p(X|Z) 尽量真实。这种方法的问题在于,这个变分后验 p(X|Z) 的表达能力与计算代价是不可兼得的。换句话说,简单的变分后验表达并不丰富(例如数学公式法),而复杂的变分后验计算过于复杂(例如PLM法)。
现在回国头来看看GAN做了啥。前面也提到过,GAN其实就是简单粗暴,没有任何encoder,直接训练生成器,唯一的难度在于判别器(就是下图这个“它们的分布相等吗”的东西)不好做。

好了,聪明的你也已经知道我要说什么了。Diffusion本质就是借鉴了GAN这种训练目标单一的思路和VAE这种不需要判别器的隐变量变分的思路,糅合一下,发现还真work了……下面让我们来看看到底是怎么糅合的。为什么我们糅合甚至还没传统方法好,大佬糅合揉出个diffusion?
Diffusion的核心
知道你们都懒得划上去,我再放一下VAE的图。

前面也已经提到,VAE的最大问题是这个变分后验。在VAE中,我们先定义了右边蓝色的生成器 X=g(Z) ,再学一个变分后验 p(X|Z) 来适配这个生成器。能不能反一下,先定义一个变分后验再学一个生成器呢?
如果你仔细看了上面的VAE部分,我相信你已经有思路了。VAE的生成器,是将标准高斯映射到数据样本(自己定义的)。VAE的后验分布,是将数据样本映射到标准高斯(学出来的)。那反过来,我想要设计一种方法A,使得A用一种简单的“变分后验”将数据样本映射到标准高斯(自己定义的),并且使得A的生成器,将标准高斯映射到数据样本(学出来的)。注意,因为生成器的搜索空间大于变分后验,VAE的效率远不及A方法:因为A方法是学一个生成器(搜索空间大),所以可以直接模仿这个“变分后验”的每一小步!
好,现在我告诉你,这个A方法就是扩散模型(Diffusion Model)的核心思路:定义一个类似于“变分后验”的从数据样本到高斯分布的映射,然后学一个生成器,这个生成器模仿我们定义的这个映射的每一小步。
Diffusion Model的Diffusion到底是个啥
接触diffusion的你肯定知道马尔可夫链!这东西不仅diffusion里面有,各种怪异的算法里面也都出现了。为什么用它?因为它的一个关键性质:平稳性。一个概率分布如果随时间变化,那么在马尔可夫链的作用下,它一定会趋于某种平稳分布(例如高斯分布)。只要终止时间足够长,概率分布就会趋近于这个平稳分布。
这个逐渐逼近的过程被作者称为前向过程(forward process)。注意,这个过程的本质还是加噪声!试想一下为什么……其实和VAE非常相似,都是在随机采样!马尔可夫链每一步的转移概率,本质上都是在加噪声。这就是扩散模型中“扩散”的由来:噪声在马尔可夫链演化的过程中,逐渐进入diffusion体系。随着时间的推移,加入的噪声(加入的溶质)越来越少,而体系中的噪声(这个时刻前的所有溶质)逐渐在diffussion体系中扩散,直至均匀。看看下面的图,你应该就恍然大悟了:
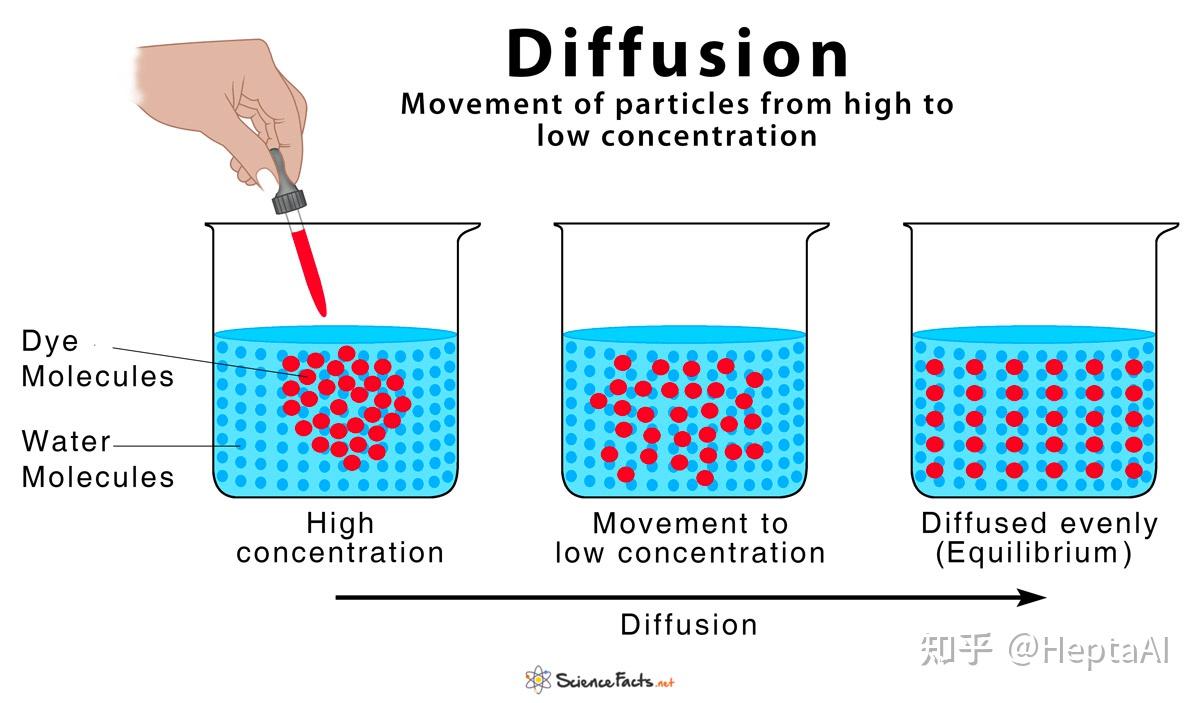
现在想想,为什么要用马尔可夫链。我们把问题详细地重述一下:为什么我们创造一个稳定分布为高斯分布的马尔可夫链,对于生成器模仿我们定义的某个映射的每一小步有帮助呢?这里你肯定想不出来,不然你也能发明diffusion model ——答案是,基于马尔可夫链的前向过程,其每一个epoch的逆过程都可以近似为高斯分布。
懵了吧,我也懵了。真正的推导发了好几篇paper,都是些数学巨佬的工作,不得不感叹基础科学的力量……相关工作主要用的是SDE(随机微分方程),我们在这里不做深入,但是需要理解大致的思路,如下图所示。
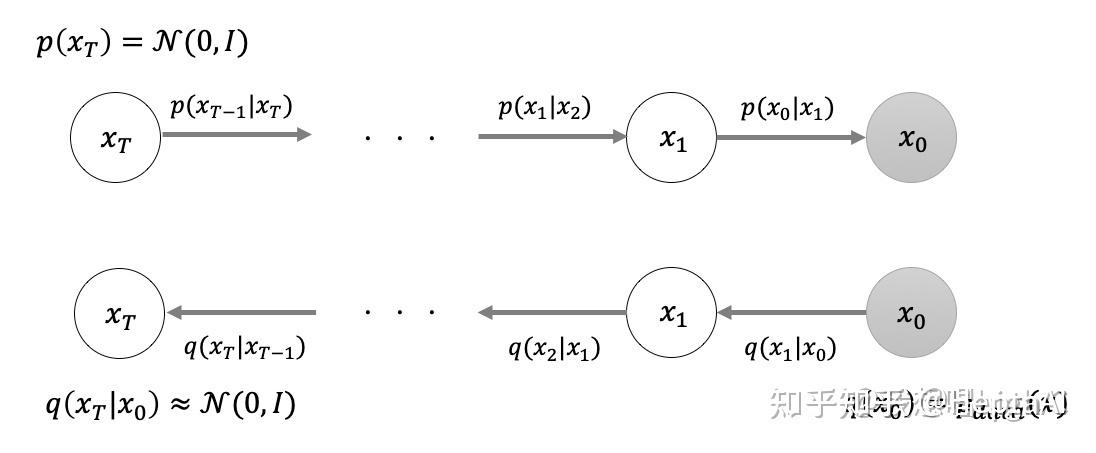
图源:https://www.zhihu.com/question/536012286/answer/2533146567
下面的是前向过程,上面的是反向过程。前向过程通过马尔可夫链的转移概率不断加入噪音,从右边的采样数据到左边的标准高斯;反向过程通过SDE来“抄袭”对应正向过程的那一个epoch的行为(其实每一步都不过是一个高斯分布),从而逐渐学习到对抗噪声的能力。高斯分布是一种很简单的分布,运算量小,这一点是diffusion快的最重要原因。
Diffusion的本质
现在回头看看diffusion到底做了个啥工作。我们着重看一下下图的VAE和diffussion的区别:
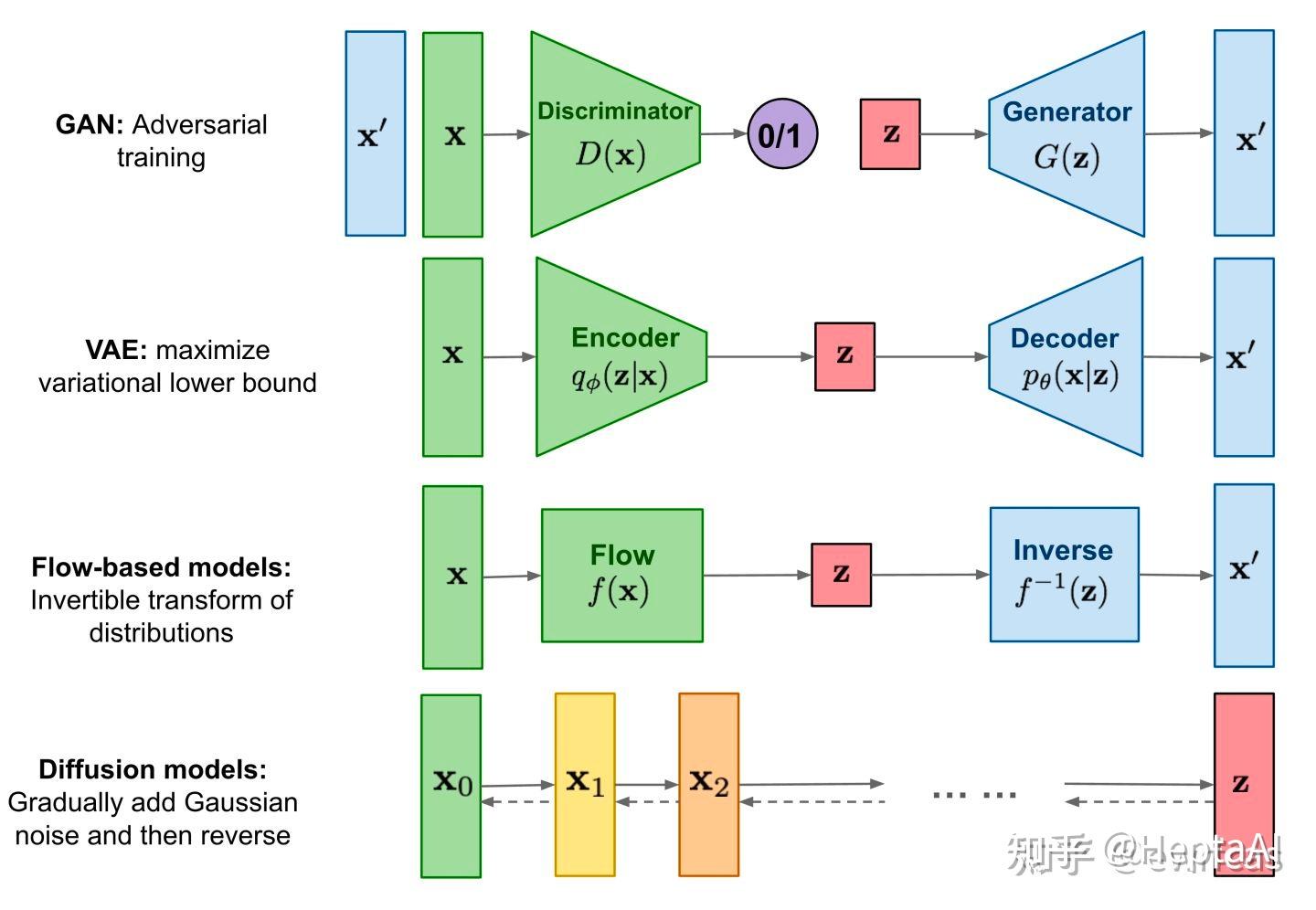
图源:https://zhuanlan.zhihu.com/p/525106459
可以很清晰的认识到,VAE本质是一个基于梯度的encoder-decoder架构,encoder用来学高斯分布的均值和方差,decoder用变分后验来学习生成能力,而将标准高斯映射到数据样本是自己定义的。而扩散模型本质是一个SDE/Markov架构,虽然也借鉴了神经网络的前向传播/反向传播概念,但是并不基于可微的梯度,属于数学层面上的创新。两者都定义了高斯分布 Z 作为隐变量,但是VAE将 Z 作为先验条件(变分先验),而diffusion将 Z 作为类似于变分后验的马尔可夫链的平稳分布。
想要更深入的理解?
如评论区指出的,文章的定位本身就是让读者读懂diffusion而非对diffusion框架本身进行数学创新,是应用向而非结构向的,大佬们如果希望看到更深入的分析可以追更和评论区催更~
参考资料 |
|